The learning parity with noise assumption (LPN) is one of the most fundamental assumptions of cryptography. It states that given a random secret vector $\vec s$ over $\mathbb{F}_2$, and given access to (an arbitrary polynomial number of) samples of the form $(\vec a, \langle \vec a, \vec s\rangle + e)$, where $\vec a$ is a random vector and $e$ is a random Bernoulli noise (i.e., $e$ is $1$ with some probability $p$, and $1$ otherwise), it is infeasible to recover $\vec s$. In other terms: while linear systems of equations are easy to solve (using Gaussian elimination), it becomes infeasible to solve them as soon as you add a bit of noise to the equations.
LPN has been widely used in cryptography, and exists in many different variants: for different noise distributions, for bounded number of samples (where it becomes equivalent to the syndrome decoding problem), for a different distribution over the $\vec a$, over a different field $\mathbb{F}$, etc. The goal of this post is not to cover variants and applications of LPN. Rather, I would like to state a very useful and folklore result regarding the security of LPN. While this result is folklore (and has been likely known for decades), I’ve not seen it stated explicitely until very recently (my coauthors and I stated it in our CRYPTO’21 paper on silent OT extension from structured LDPC codes, see my publication page). Since I believe it’s a useful observation and guiding principle when analyzing the security of LPN variants, I decided to make a post about it. What follows is essentially taken from our CRYPTO’21 paper.
A Generalized LPN Assumption
we define the LPN assumption over a ring $\mathcal{R}$ with dimension $k$, number of samples $n$, w.r.t. a code generation algorithm $\mathsf{CodeGen}$, and a noise distribution $\mathcal{D}$:
Let $\mathcal{D}(\mathcal{R}) = \{\mathcal{D}_{k,n}(\mathcal{R})\}_{k,n\in\mathbb{N}}$ denote a family of efficiently sampleable distributions over a ring $\mathcal{R}$, such that for any $k,n\in\mathbb{N}$, $\mathsf{Image}(\mathcal{D}_{k,n}(\mathcal{R}))\subseteq\mathcal{R}^n$. Let $\mathsf{CodeGen}$ be a probabilistic code generation algorithm such that $\mathsf{CodeGen}(k,n,\mathcal{R})$ outputs a matrix $A\in \mathcal{R}^{n\times k}$. For dimension $k=k(\lambda)$, number of samples (or block length) $n=n(\lambda)$, and ring $\mathcal{R} = \mathcal{R}(\lambda)$, the (primal) $(\mathcal{D},\mathsf{CodeGen},\mathcal{R})\text{-}LPN(k,n)$ assumption states that
$\{(A, \vec{b}) \;|\; A\gets_r\mathsf{CodeGen}(k,n,\mathcal{R}), \vec{e}\gets_r\mathcal{D}_{k,n}(\mathcal{R}), \vec{s}\gets_r\mathbb{R}^k, \vec{b}\gets A\cdot\vec{s} + \vec{e}\}$
\[\approx \{(A, \vec{b}) \;|\; A\gets_r\mathsf{CodeGen}(k,n,\mathcal{R}), \vec{b}\gets_r\mathcal{R}^n\}.\]The above definition is very general, and captures in particular not only the standard LPN assumption and its variants, but also assumptions such as LWE or the multivariate quadratic assumption. However, we will typically restrict our attention to assumptions where the noise distribution outputs sparse vectors with high probability. The standard LPN assumption with dimension $k$, noise rate $r$, and $n$ samples is obtained by setting $A$ to be a uniformly random matrix over $\mathbb{F}_2^{n\times k}$, and the noise distribution to be the Bernoulli distribution $\mathsf{Ber}^n_r(\mathbb{F}_2)$, where each coordinate of $\vec e$ is independently set to $1$ with probability $r$ and to $0$ with probability $1-r$. The term primal in the above definition comes from the fact that the assumption can come in two equivalent form: the primal form as above, but also a dual form: viewing $A$ as the transpose of the parity check matrix $H$ of a linear code generated by $G$ a matrix, i.e. $A=H^\intercal$, the hardness of distinguishing $H^\intercal \cdot \vec x + \vec e$ from random is equivalent to the hardness of distinguishing $G\cdot (H^\intercal \cdot \vec x + \vec e) = G \cdot \vec e=\vec e\cdot G^\intercal$ from random (since $G^\intercal \cdot H = 0$).
Core Observation
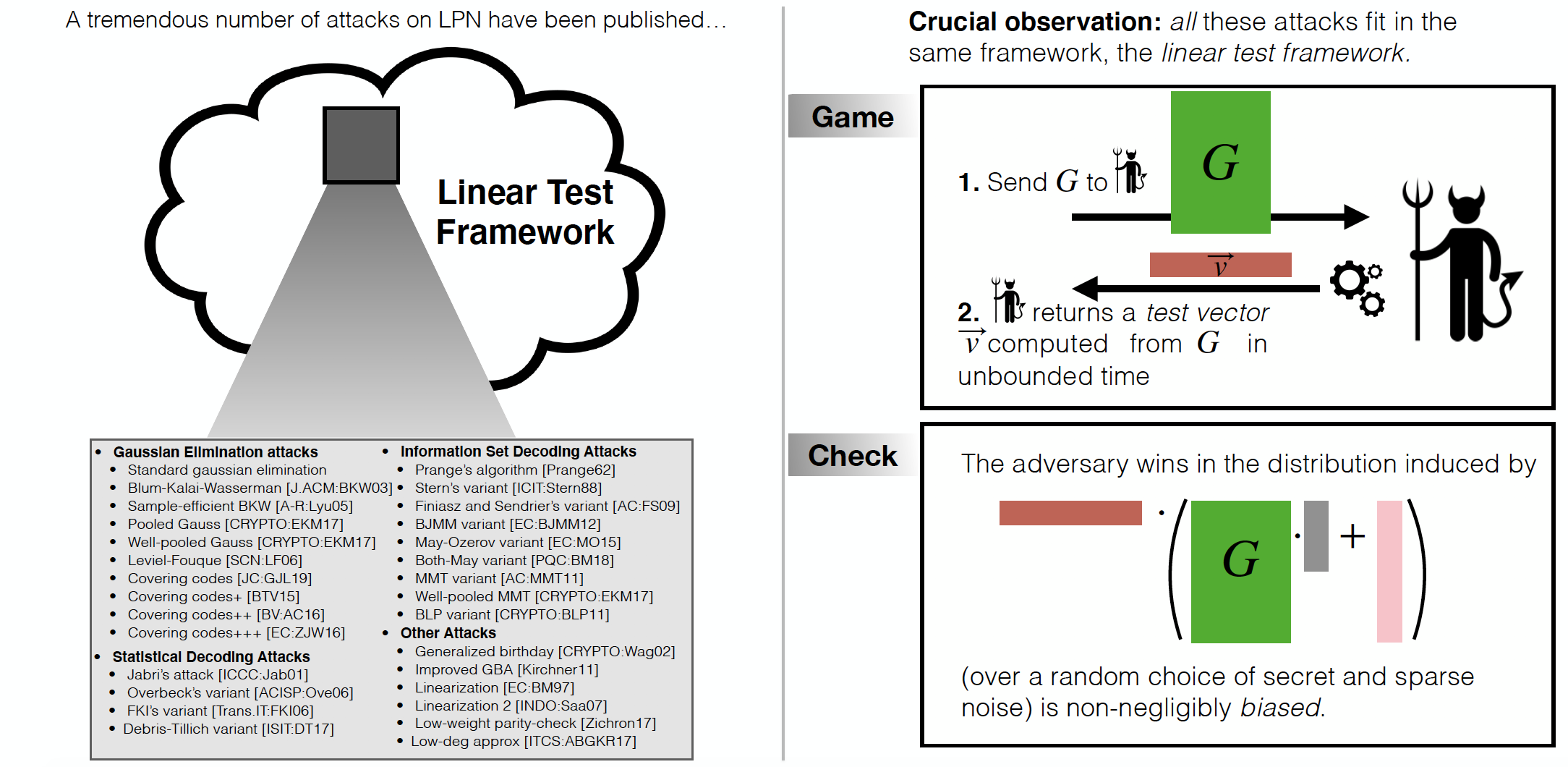
Over the past few decades, a tremendous number of attacks against LPN have been proposed. These attacks include, but are not limited to, attacks based on Gaussian elimination and the BKW algorithm (and variants based on covering codes), information set decoding attacks, statistical decoding attacks, generalized birthday attacks, linearization attacks, attacks based on finding low weight code vectors, or on finding correlations with low-degree polynomials.
In light of this situation, it would be excessively cumbersome, when introducing a new variant of LPN, to go over the entire literature of existing attacks and analyze their potential impact on the new variant. The crucial observation, however, is that this is not necessary, as all the above attacks (and more generally, essentially all known attacks against LPN and its variants) fit in a common framework, usually denoted the linear test framework. Furthermore, the asymptotic resistance of any LPN variant against any attack from the linear test framework can be deduced from two simple properties of the underlying code ensemble and noise distribution. Informally, if
- the code generated by $G$ has high minimum distance, and
- for any large enough subset $S$ of coordinates, with high probability over the choice of $\vec e \gets \mathcal{D}$, at least one of the coordinates in $S$ of $\vec e$ will be nonzero,
then the LPN assumption with code matrix $G$ and noise distribution $\mathcal{D}$ cannot be broken by any attack from the linear test framework.
The Linear Test Framework
The common feature of essentially all known attacks against LPN and its variants is that the distinguisher can be implemented as a (nonzero) linear function of the samples (the linear test), where the coefficients of the linear combination can depend arbitrarily on the code matrix. Therefore, all these attacks can be formulated as distinguishing LPN samples from random samples by checking whether the output of some linear test (with coefficients depending arbitrarily on the code matrix) is biased away from the uniform distribution. Formally,
Security Against Linear Tests. Let $\mathbb{F}$ be an arbitrary finite field, and let $\mathcal{D} = \{\mathcal{D}_{m,n}\}_{m,n\in\mathbb{N}}$ denote a family of noise distributions over $\mathbb{F}^n$. Let $\mathsf{CodeGen}$ be a probabilistic code generation algorithm such that $\mathsf{CodeGen}(m,n)$ outputs a matrix $A\in \mathbb{F}^{n\times m}$. Let $\varepsilon, \delta: \mathbb{N} \mapsto [0,1]$ be two functions. We say that the $(\mathcal{D},\mathsf{CodeGen},\mathbb{F})\text{-}LPN(m,n)$ assumption with dimension $m = m(\lambda)$ and $n = n(\lambda)$ samples is $(\varepsilon,\delta)$-secure against linear tests if for any (possibly inefficient) adversary $\mathcal{A}$ which, on input a matrix $A\in \mathbb{F}^{n\times m}$, outputs a nonzero $\vec v \in \mathbb{F}^n$, it holds that
$\Pr[A \gets_r \mathsf{CodeGen}(m,n), \vec v \gets_r \mathcal{A}(A)\;:\; \mathsf{bias}_{\vec v}(\mathcal{D}_{A}) \geq \varepsilon(\lambda) ] \leq \delta(\lambda),$
where $\mathsf{bias}$ denotes the bias of the distribution (the bias of a distribution is defined as $\mathsf{bias}(\mathcal{D}) = \max_{\vec u \neq \vec 0} |\mathbb{E}_{\vec x \sim \mathcal{D}}[\vec u^\intercal \cdot \vec x] - \mathbb{E}_{\vec x \sim \mathcal{U}_n}[\vec u^\intercal \cdot \vec x]|$), and $\mathcal{D}_{A}$ denotes the distribution induced by sampling $\vec s \gets_r \mathbb{F}_2^m$, $\vec e \gets \mathcal{D}_{m,n}$, and outputting the LPN samples $A\cdot \vec s + \vec e$.
Now, define the dual distance of a matrix $M$, written $\mathsf{dd}(M)$, to be the largest integer $d$ such that every subset of $d$ rows of $M$ is linearly independent. The name dual distance stems from the fact that the $\mathsf{dd}(M)$ is also the minimum distance of the dual of the code generated by $M$ (i.e., the code generated by the left null space of $M$). The following lemma is folklore:
Lemma: For any $d\in \mathbb{N}$, the $(\mathcal{D},\mathsf{CodeGen},\mathbb{F})\text{-}LPN(m,n)$ assumption with dimension $m = m(\lambda)$ and $n = n(\lambda)$ samples is $(\varepsilon_d,\delta_d)$-secure against linear tests, where
- $\varepsilon_d = \max_{\mathsf{HW}(\vec v) > d}\mathsf{bias}_{\vec v}(\mathcal{D}_{m,n})$, and
- $\delta_d = \Pr_{A \gets_r \mathsf{CodeGen}(m,n)}[\mathsf{dd}(A) \geq d]$.
($\mathsf{HW}(\vec v)$ denotes the Hamming weight of $\vec v$)
Proof : The proof is straightforward: fix any integer $d$. Then with probability at least $\delta_d$, $\mathbb{dd}(A) \geq d$. Consider any (possibly unbounded) adversary $\mathcal{A}$ outputting $\vec v$. Two cases can occur:
- Either $\mathsf{HW}(\vec v) \leq d \leq \mathsf{dd}(A)$. In this case, the bias with respect to $\vec v$ of the distribution $\{A \cdot \vec s \;|\; \vec s \gets_r \mathbb{F}^m\}$ is $0$ (since this distribution is $d$-wise independent). Since the bias of the XOR of two distribution is at most the smallest bias among them, we get $\mathsf{bias}(\mathcal{D}_{A}) = 0$.
- Or $\mathsf{HW}(\vec v) > d$; in which case $\mathsf{bias}(\mathcal{D}_A) \leq \mathsf{bias}(\mathcal{D}_{m,n})$.
The above follows directly from simple lemmas on bias, which are recalled in my cheat sheet.
Example: Standard LPN with Random Code and Bernoulli Noise
An instructive example is to consider the case of LPN with a uniformly random code matrix over $\mathbb{F}_2$, and a Bernoulli noise distribution $\mathcal{D}_{m,n} = \mathsf{Ber}^n_r(\mathbb{F}_2)$, for some noise rate $r$. The probability that $d$ random vectors over $\mathbb{F}_2^m$ are linearly independent is at least
\[\prod_{i=0}^{d-1} \frac{2^m - 2^i}{2^m} \geq (1-2^{d-1-m})^d \geq 1 - 2^{2d - m}.\]Therefore, by a union bound, the probability that a random matrix $A \gets_r \mathbb{F}_2^{n\times m}$ satisfies $\mathsf{dd}(A) \geq d$ is at least $1 - {n \choose d}\cdot 2^{2d - m} \geq 1 - 2^{(2+\log n)d - m}$. On the other hand, for any $d$ and any $\vec v$ with $\mathsf{HW}(\vec v) > d$, we have by the piling-up lemma (see the cheat sheet):
\[\Pr[\vec e \gets \mathsf{Ber}^n_r(\mathbb{F}_2)\; : \; \vec v^\intercal \cdot \vec e = 1] = \frac{1 - (1-2r)^d}{2},\]hence $\mathsf{bias}_{\vec v}(\mathsf{Ber}^n_r(\mathbb{F}_2)) = (1-2r)^d \leq e^{-2rd}$. In particular, setting $d = O(m/\log n)$ suffices to guarantee that with probability at least $\delta_d = 1 - 2^{-O(m)}$, the LPN samples will have bias (with respect to any possible nonzero vector $\vec v$) $\varepsilon_d$ at most $e^{-O(rm/\log n)}$. Hence, any attack that fits in the linear test framework against the standard LPN assumption with dimension $m$ and noise rate $r$ requires of the order of $e^{O(rm/\log n)}$ iterations. Note that this lower bound still leaves a gap with respect to the best known linear attacks, which require time of the order of $e^{O(rm)}$, $e^{O(rm/\log \log m)}$, and $e^{O(rm/\log m)}$ when $n = O(m)$, $n = \mathsf{poly}(m)$, and $n = 2^{O(m/\log m)}$ respectively.
It is straightforward to extend the above to general fields, but I’ll leave that as an exercise to the reader ;)
]]>